
RACIONALIZACIÓN
¡Vamos a emprender esta aventura matemática juntos!


¿Qué es la racionalización?
La racionalización Esta consiste en eliminar las raíces que se encuentran en el denominador de una fracción,lo que permite facilitar el cálculo de operaciones como la suma de fracciones, la resta, multiplicación o división .Básicamente es encontrar otra expresión equivalente que no tenga raíces en el denominador.
Para ello se multiplica el numerador y el denominador por la expresión que se requiera, de manera que cuando se opere la raíz del denominador quede simplificada.

Casos de racionalización
-
Racionalización de un monomio
-
Racionalización de monomios con índices mayores que 2
-
Racionalización de binomio
-
Racionalización de binomios con radical mayor a 2
Racionalización de un monomio
Básicamente, lo que necesitamos hacer es completar la potencia del radicando para que quede con el mismo valor que el índice, y así poder cancelar la raíz. En este ejemplo como podemos ver el radicando es de potencia 1 ,y el índice de la raíz es 2, lo que tenemos que hacer es hallar la manera de que el radicando tenga potencia 2 para simplificar la raíz."
*En pocas palabras es amplificar la fracción por el denominador*"

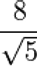
radicando
Entonces para lograr esto, multiplicamos por el mismo denominador a toda la fracción

Aquí usamos la regla de la potenciación a^m x a^n=a^m+n
Para operar exponentes

Entonces al sumar los exponentes nos da 2 por lo tanto el radicando queda elevado al cuadrado
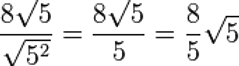
Ahora como el radicando tiene el mismo valor numérico que el índice podemos cancelar la raíz y queda solucionado este ejercicio.

Racionalización de un monomio de la forma


Es hacer casi hacer lo mismo que en el proceso anterior, lo que podemos notar es que un término del denominador no tiene raíz y está multiplicando al término que si la tiene. Entonces lo que tenemos que hacer para deshacernos de esa raíz es multiplicar toda la fracción SÓLO por el término que tiene la raíz, observa."

Monomios con índice mayor a dos

¡Continuemos! Si nos damos cuenta no es tan difícil como parece, ahora veremos racionalización de un monomio por un índice mayor de 2.
Como ya habíamos dicho antes, racionalizar básicamente es completar el índice del radicando para deshacernos de la raíz, en este ejercicio notarás cómo se ejerce esta afirmación.

Como sabemos 2^2 da 4 entonces lo expresamos de esa manera para que sea más fácil completar la raíz
Aquí vamos a completar el indice del radicando con lo que le falta para que sea igual al de la raíz
Aquí usamos la regla de la potenciación
a^m x a^n=a^m+n
Racionalización de un binomio
Para racionalizar este ejercicio usaremos el conjugado del denominador para utilizar el producto notable de " Producto de dos binomios conjugados", el cual nos dará una diferencia de cuadrados. obseva:



Si nos damos cuenta es muy similar al proceso anterior, simplemente es utilizar el conjugado y el producto notable; este al darnos una diferencia de cuadrados nos permite cancelar la raíz, y cuando esto ocurre simplemente se opera .


Binomio con índice mayor a 2
Ahora, el siguiente caso es "racionalización de binomios con índices mayores que dos".
Para cuando se tienen este tipo de binomios es preciso utilizar productos notables, observa :

Aquí se multiplica la fracción por el resultado del producto notable con su conjugado

(Resultado)

Ahora, se resuelven las potencias que están fuera del paréntesis (observa bien el numerador):

Ahora, el denominador se transforma en producto notable:


Ya que los exponentes de las cantidades radicales del denominador son iguales o múltiplos de 3, se procede al despeje del radical del denominador, que es el último paso de la racionalización:



